
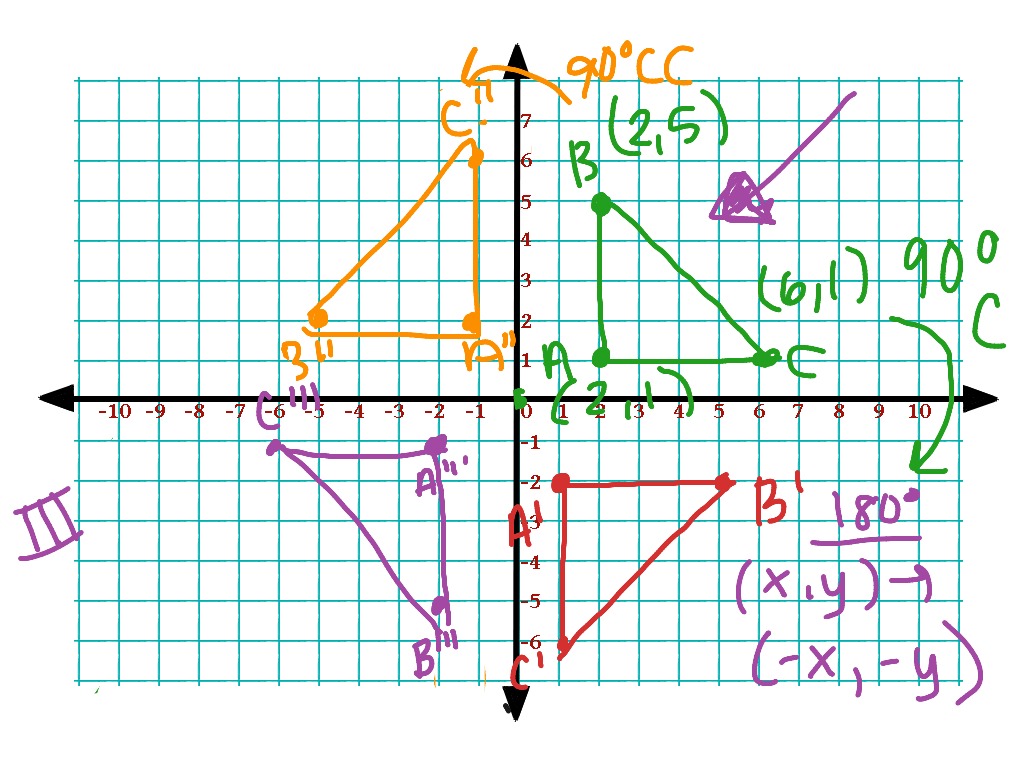
Rotate 180 counterclockwise (same as 180 clockwise) (x. When a point (a, b) is rotated counterclockwise about the origin, the following are. Identify whether or not a shape can be mapped onto itself using rotational symmetry. Rotations: Rotate 90 counterclockwise (same as 270 clockwise) (x, y) (y, x).Describe the rotational transformation that maps after two successive reflections over intersecting lines.Describe and graph rotational symmetry.The are the same thing and you will use the same formula. In the video that follows, you’ll look at how to: There is no difference between 90-degree Clockwise Rotation and 270-degree counter clockwise rotation. a 90 degree rotation (counterclockwise of course) makes it be on the y axis instead at (0,1). The most common rotations are usually 90, 180 and 270. Take the point (1,0) thats on the x axis.
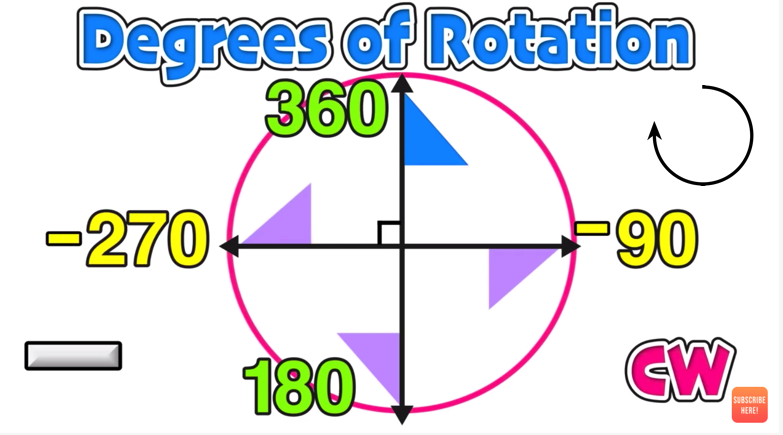
You can find both the Clockwise and AntiClockwise directions of rotation by the rotation calculator. The order of rotations is the number of times we can turn the object to create symmetry, and the magnitude of rotations is the angle in degree for each turn, as nicely stated by Math Bits Notebook. Clockwise and AntiClockwise Rotation Rules: We need to understand that the rotation can be done in both Clockwise and AntiClockwise directions. And when describing rotational symmetry, it is always helpful to identify the order of rotations and the magnitude of rotations. This means that if we turn an object 180° or less, the new image will look the same as the original preimage. Clearly, the correct right image is in option 1). Lastly, a figure in a plane has rotational symmetry if the figure can be mapped onto itself by a rotation of 180° or less. Note: It is first rotated through 90 in a clockwise direction.


 0 kommentar(er)
0 kommentar(er)
